Simpson’s Rule

The generic form of a parabola is .

The area of the parabolic region from to is

Find , , and by substituting the x-values at those points

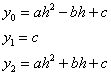
Add the and

Substituting into the area equation above gives

So, the area of the parabolic region can be found by adding first y-value, , four times the middle y-value, , and the last y-value, , then multiplying that sum by one-third of the interval width, h.

Thus, given an odd number of x-values, , the area of the region can be estimated by

Factor out the , replace h with , and combine like terms to get Simpson’s Rule: